E' fondamentale convincersi che devono essere indipendentemente nulle sia la somma delle forze sia la somma dei loro momenti. Una forza compare quindi due volte, sia quando la si somma alle altre nel tentativo di dare risultante nulla per non far traslare il corpo rigido, sia quando ne si calcola il momento (talvolta nullo) per poter poi calcolare la somma dei momenti, da mettere a zero per non far ruotare il corpo.
A questo punto veniamo all'elicottero. Una cosa da capire dell'elicottero è che il rorore principale esercita una forza
solo lungo il suo asse di rotazione, e questa forza, a giri costanti, è tanto più intensa quanto più è alto il passo collettivo. Inoltre, dato che questa forza è allineata con il baricentro, ha braccio nullo e quindi momento nullo, cioè non tende a far ruotare l'elicottero in nessun modo. Interesserà quindi solo la traslazione. Il ciclico invece è in grado di produrre una coppia di forze, da un lato il rotore è spinto a salire e dall'altro a scendere. Sono due forze uguali e contrarie, quindi anche se hanno punto di applicazione diverso la loro somma vettoriale è nulla. Ai fini della traslazione quindi non servono assolutamente a nulla (ecco perché il ciclico non fa traslare l'eli). Però la somma dei loro momenti (che è ben diversa dal momento della loro somma, che è appunto zero) è tutt'altro che nulla, quindi fa ruotare il rotore, cioè lo inclina, permettendogli di spingere l'elicottero nella direzione voluta. Quindi:
collettivo > forza sì, momento no
ciclico > forza no (è una coppia con risultante nulla), momento sì
Invece il rotore di coda ha entrambi gli effetti, perché oltre ad essere una forza semplice non bilanciata ha anche un braccio non nullo rispetto al baricentro.
Non mi resta che rivedere ciò che succede sull'elicottero. Devo rifarlo per mettere in luce l'utilità delle lunghe premesse appena scritte, ma i disegni della volta scorsa restano validi e utilissimi. Affrontiamo prima le rotazioni, quindi ciò che riguarda la seconda equazione, quindi i momenti. Il rotore principale viene frenato dall'aria, cioè subisce un momento che si oppone alla sua rotazione. Questo momento nasce dalla forza (esterna) d'attrito che l'aria produce sul rotore principale, quindi va bilanciato dal momento di un'altra forza esterna. Poco importa che di mezzo ci sia il principio di azione e reazione applicato al motore che spinge il rotore e quindi viene (insieme al resto dell'eli) da lui spinto. Il passaggio della patata bollente giunge al rotore di coda che è l'unico in grado, spingendo l'aria e quindi venendo spinto da essa, di procurarci la forza esterna di cui abbiamo bisogno. Questa forza esterna, grazie al braccio che la separa dall'asse del rotore principale, ha infatti un momento uguale e contrario a quello esercitato dall'aria che frena il rotore principale. Se il rotore di coda è alla stessa altezza del
baricentro (il centro del rotore principale non ha alcun significato importante) non esercita momenti di rollio, solo di imbardata. Ma se non è così, e quindi genera un momento di rollio, basta generare col ciclico una coppia contraria per impedire questo rollio (dalla seconda equazione la "somma dei momenti di rollio nulla" implica "nessuna accelerazione di rollio", che non vuol però dire rotore orizzontale, ma rotore che non si muove: se è inclinato, come vedremo che è, ci rimane).
Con le rotazioni abbiamo finito, rimangono le traslazioni, prima equazione. Ma a questo punto è facilissimo: ci sono la forza peso e la forza del rotore di coda che non possiamo abolire, le dobbiamo bilanciare. Chi se ne occupa, di entrambe, è il rotore principale, che deve esercitare una forza che scomposta sui due assi ci dà:
sulla verticale una spinta uguale e contraria al peso: l'eli né sale né scende
sulla orizzontale una spinta uguale e contraria a quella del rotorino: l'eli non trasla di lato
Per avere contemporaneamente queste due componenti il rotore principale
deve essere inclinato, perché l'unica forza viva che lui esercita è tramite il collettivo, e questa forza è diretta lungo il suo asse di rotazione. Visto che la forza deve avere una componente orizzontale l'asse di rotazione
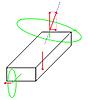
non può essere esattamente verticale. Per l'occasione mi sono messo d'impegno e ho inclinato nella figura il rotore come deve essere (anche il parallelepipedo si dovrebbe inclinare dello stesso angolo, ma con paint non sono proprio in grado), così si dovrebbe capire perfettamente com'è la situazione traslatoria dell'eli.
THE END
Ora, quello che ho scritto è la verità, mi auguro che abbiate la voglia di meditarci un po' (non pensate che per me sia scienza infusa, me le sono dovute spremere le meningi per studiare 'sta roba) e soprattutto alla fine crederci. Io vi dico che ne sono sicuro (nei limiti di qualche imprecisione o di effetti terziari volutamente trascurati). Normalmente vado cauto in quello che affermo, chiedo sempre se l'interlocutore concorda e così via, ma questa volta siamo nel mio campo e non nutro più alcun dubbio. Aspetto solo di discutere su eventuali esperimenti o su cose che mi sono dimenticato di dire, ma per il resto la risposta la trovate qui sopra e al
post 18. Passo e chiudo.